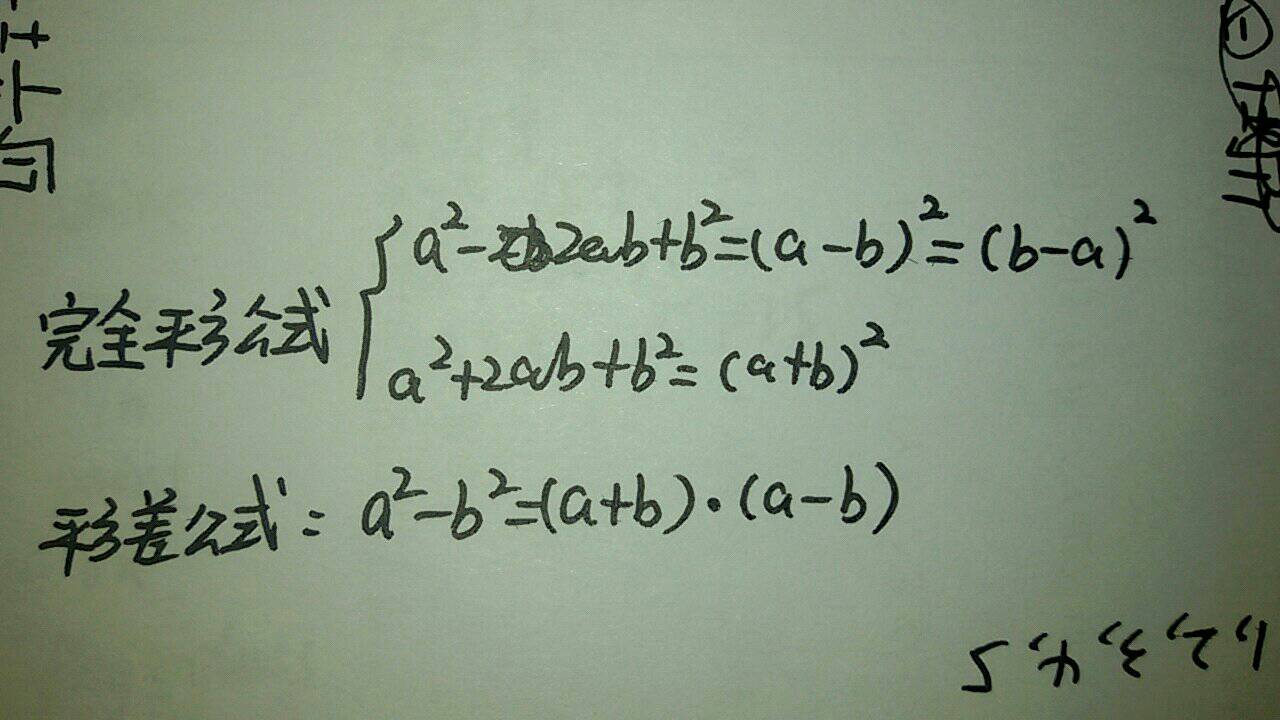乘方的公式
的有关信息介绍如下:同底数幂相乘除,原来的底数作底数,指数的和或差作指数。
【 a^m*a^n=a^(m+n)】
推导:
设a^m*a^n中,m=2,n=4,那么
a²*a⁴
=(a*a)*(a*a*a*a)
=a*a*a*a*a*a
=a⁶
=a²⁺⁴
所以代入:a^m*a^n=a^(m+n)
用字母表示为:
a^m·a^n=a^(m+n) 或 a^m÷a^n=a^(m-n) (m、n均为自然数)
例如:
1)15²×15³; 2)3²×3⁴×3⁸; 3)5×5²×5³×5⁴×…×5⁹⁰
1)15²×15³=15²⁺³=15⁵
2)3²×3⁴×3⁸=3²⁺⁴⁺⁸=3¹⁴
3)5×5²×5³×5⁴×…×5⁹⁰=5¹⁺²⁺³⁺…⁺⁹⁰=5⁴⁰⁹⁵ a⁰=1 ,其中a≠0 ,k∈N*
推导:
a⁰
=a¹⁻¹
=(a¹)/(a¹)
=a/a
=1 【 a^(-k)=1/(a^k) 】,其中a≠0,k∈N*
推没氏导:
a^(-k)
=a^(0-k)
=(a^0)/(a^k)
=1/(a^k) 【 a^[-(m/n)]= 】,其中,a^m≠0( ≠0,a≠0),m/n>0,n≠0,m,n∈N*
推导:
a^[-(m/n)]
=a^(0-m/n)
=(a^0)/[a^(m/n)]
=1/[a^(m/n)]
=1/
=
分数指数幂时,当n=2k,k∈N*, 且a^m<0时,则该数在实数范围内无意义
特别地,0的非正数指数幂没有意义 两数和乘两数差等于它们的平方差。
用字母表示为:
【(a+b)(a-b)=a²-b²】
推导:
(a+b)(a-b)
=(a+b)a-(a+b)b
=(a²+ab)-(b²+ab)
=a²-b² (a/b)^k=a^k/b^k
证模旦明:(a/b)^k=a^k*b^-k=a^k/b^k 幂的乘方,底数不变,指数相乘。
用字母表示为:
【(a^m)^n=a^(m×n) 】
特别指出:a^m^n=a^(m^n) 积的乘方,先把积中的每一个因数分别乘方,再把所得的幂相乘。
用字母表示为:
【 (a×b)ⁿ=aⁿ×bⁿ 】
这个积的乘方法则也适用于三个以上乘数积的乘方。如:
(a×b×c)ⁿ=aⁿ×bⁿ×cⁿ
同指数幂乘法
同指数幂相乘,指数不变,底数相乘。
用字母表示为:
(aⁿ)*(bⁿ)=(ab)ⁿ 两数和(或差)的平方,等于它们的平方的和加上(或者减去)它们的积的2倍。
用字母表示为:
【 (a±b)²=a²±2ab+b² 】
我们一般把它叫作完全平方公式 。
艾萨克·牛顿发现了二项式。二项式是乘方里的复杂运算。右图为二项式计算法则。一般来说,二项式的各项系数按排列顺序也可以这样表示:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
…… …… ……
这就是著名的杨辉三角。 (1)负数的偶次幂是正数,负数的奇数幂是负数。
( 2)正数的任何次幂都是正数。
(3)0的任何旦察扰正整数次幂都是0。