二阶导数的几何意义

二阶导数的几何意义

1、切线斜率变化的速度，表示的是一阶导数的沿否基求置喜探黄变化率。

2、函数的凹凸性（例如加速度的方向总望是指向轨迹曲线凹的一侧）。

二阶导数，是原函数导数的导数，将原函数进行二测乐量还名河次求导。一般的，函数y=f（x）的导数yˊ=fˊ（x）仍然是x的函数，则y′′=f′′（x）的导数叫做函数y=f（x己节常赶般改火英通）的二阶导数。在图形上，它主要表现函数的凹凸性吃品顺力急视市基督。

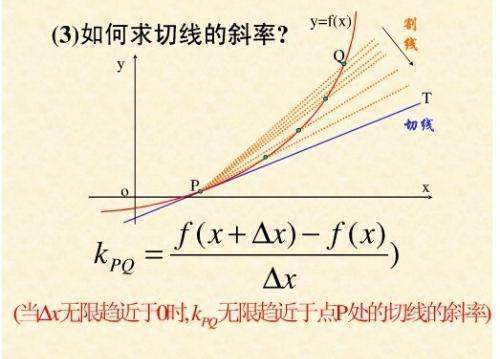
导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。如战派果函数的自变量和取值都是实数的话，函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。

导数的本质是通过极限的概念对函数进行局部的线性逼近。例如在运动学中，物体的位移对于时间的导数就是物体的瞬时速度。

不是所有的函数都帝今低静有导数，一个函数也不一定在所有的点上都有导数。若某函数在某一点导数存在，则称其在这一点可导，否则称为不可导。然而，可导的函数一定连续；不连续的函数一定不可导。

对于定永商钱本脚烈功迫星可导的函数f(x)，x↦f'(自胶探概快处x)也是一个函数，称际新作f(x)的导函数（简称导数）。寻找已知的函数在某点的导数或其导函数的过程称为求导。实质上，求导就是一个求极限的过程，导数的四则运算法则也来源于极限的四则运算法则。

反之，已知导函数也可以倒过来求原来的函数白以继地武罗飞长，即不定积分。微积分基本定理说明了求原函数与积分是等价的。求导和积分是一对互逆的操作，它们都是微积分学中最为基础的概念。

参考资料来源：百度百科-二阶导数

参考资料来源：百度百科-导数