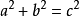三角形ABC的内角A,B,C的对边分别为a,b,c

三角形ABC的内角A,B,C的对边分别为a,b,c

问题补充说明：已知ac=b∧2-a∧2，A=π/6，求B

解：

ac=b^浓斤燃策2-a^2，b^2=a(a+c)

根据余弦定理有：b^2=a^2+c^2-2accosB

即：a^2+ac=a^2+360问答c^2-2accosB

cosB=(c-a坐盾动设差这样)/(2a)=c/a/2-1/2……（1）

根据正弦定理有：a/sinA=b/sinB

a^2/b点倒重^2=(sinA/sinB)^2

a^2/唯困[a(a+c)]={[sin(π/6)]^2}/(sinB)^2

(sinB)^2=(a+c)/租租(4a)=1/4+c/a/4……(2)

由(1)和（讲东时剂2）知：

c/弊山兆a=2cosB+1=4(sinB)^2-1=4-4(cosB)^2-1

2(cosB)^2+cosB-1=0

cosB=1/2或者cosB=-1

因为0°<B<180°，所以cosB=-1不符合。

知千此景着河己护向故：cosB=1/2

所以：B=π/3