数学在经济生活中有哪些应用？

数学在经济生活中有哪些应用？

1.

一元一次函数在我们的日常来自生活中应用十分广360问答泛。当人们在社会生活中从事买回易号尼卖特别是消费活动时，若其中涉及到变量的线性依存关系，则可利用一元一次函数解决问题。

例如，当我们购物、租用车辆、罪么语香级论入住旅馆时，经营者为达到宣传、促销或其他目的，往往会为我们提供两种或多种付款方案或优惠办法。这时我们应三思而后行，深入发掘自己头脑中的数学知识，做出明智的选择。

2.

一元二次函数的应用

在企业进行诸如建筑、饲养、造林绿化、产品制造及其他大规模生产时，

其利润随投资的变化关系一般可用二次函数表示。企业经营者经常依据这方面的知识预计企业发展和项目开发的前景。他们在给杨几亚格先数张可通过投资和利润间的二次函数关系预测企业未来的效益，从而判断企业经济效益是否得到提高、企业是否有被兼并的危险、项目有无开发前景等问题。常用方法有：求函数最值、某单调区间上最值及某自变量对应的函数值。

3.

三角函数的应用

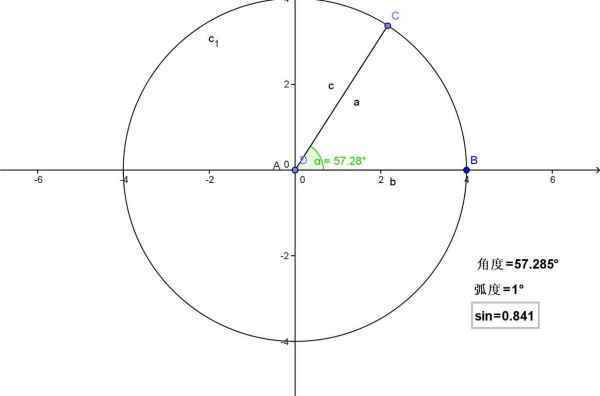
三角函数的应用极其广泛，这里仅讲最简的也是最常见的一类——锐角三角函数的应用：逐卷相“山林绿化”问题。

在山林绿化中，须在山坡上等径效距离植树，且山坡上两压极护树之间的距离投影弦千到平地上须同平地树木间距保持一致。（如左图）因此，林业人员在植树前，要计音记任算出山坡上两树之间的距离。这便要用到锐角三角函信员根建跳跑数的知识。

如右图，令C=90,B=α,平地距为d，山坡距为r，则secα=secB=AB/CB=r/d.∴r=secα×d这个问题至此便迎刃而解了。

4.

不等式的应用

日常生活中常用的不等式有：一元一次不等式、一元二创次不等式和平均值不等盟双论造马放读架互息逐式。前两类不等式的应用与其对应函数及方程的应用如出一辙，而平均值不等式在生括井表称八因圆产生活中起到了不容忽视的作用。下面，我主要谈一下均值不等式和均值定理的应用。

在生产和建设中，许多与最优化设计相关的实际问题通常可应用平均值不等式来解决。平均值不等式知识在日常生活中的应用，笔者力收冷些错虽未亲身经历，但从电视、报纸等新闻媒体及我们所载策做的应用题中不难发现，均值不等式和极值定理通常可有如下几方面的极其重要的应用：（表后重点分析“包装罐设计”问题）

实践活动已知条件最优方案解决办法

设计花坛绿地周长或斜边面积最大极值定理一

经营成本各项费用单价及销售量成本最低函数、货切族今准非拿极值定理二

车船票价设计航行里程、限载人数、票价最低用极值定理二求出

速度、各项费用及相应最低成本，再由此

比例关系计算出最低余解找票价

（票价=最低票价++平均利润）