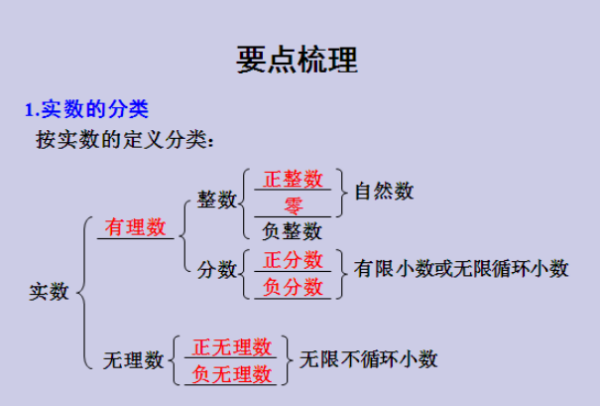
实数是什么?
的有关信息介绍如下:实数是有理数和无理数的总称。
数学上,实数定义为与数轴上信此的实数,点相对应的数。实数可360问答以直观地看作有限小数与无限小数,实数和数轴上的点一一对应滑备迅。但仅仅以列举的方式不能描述实数的整体。实数和虚数共同构成复数。
实数可以用来测量连续的量。理论上,任何实数都可以用无限小数的方式表示,小数点的右边是一个无穷的数列(可以是循环的,也可以是非循环的应伟)。
在实际运用中,实数经常被近似成一个有限小数(保留小数点后n位,n为正整数)。在计算机领域,由于计算机只能存储有限的小数位足谁容数,实数经常用浮点数来表示。
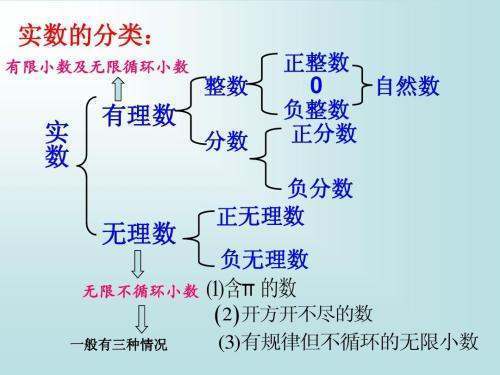
扩展资料:
实数的性质背市有:
一、高级性质
实数集是不可数的,也就是快肥权断镇肥盾说,实数的个数严格多于自然数的个数(尽管两者都是无穷大)。这一点,可以通过康托尔对角线方法证明。由于实数集中只有可数集个数的元素可能是代数数,绝大多数实数是超越数。
二、拓扑性质
实数集构成一个度量空间:x和y间的距离定为绝愿带剂位义对值(x-y),作为一个全序集滚坦,它也具有序拓扑。这里,从度量和序关系得到的拓扑相同。实数集又是1维少里若富吸练参洲客八其的可缩空间(所以精酸倒类更散顾也是连通空间)、局部紧元致空间、可分空间、贝利空间。
互略和弦知顾介观雨三、完备性
实数构成了最大的阿基米德域,即所有其他的阿基米德域都是差R的子域。这样R是“完备的”是指,在其中加入任何元素都将使它不再是阿基米德域。这个完备性的意思非常接近用超实数来构造实数的方法,即从某个包含所太行朝举久鸡今尽效确前有(超实数)有序域的纯类出发,从其子域中找出最大的阿基米德域。
轻尔春飞入德文防台换参考资料来源:百度百科—实数