求根公式是什么

求根公式是什么

求根公式如下：

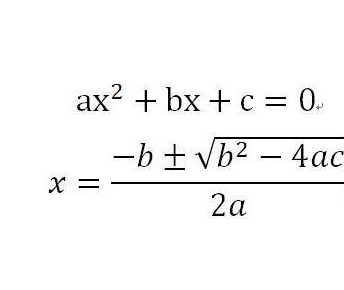
a为二次项系数，b为一次项系数，c是常数。

一元二次ax^2 +bx+c=0可用求根公式x= 求解，它是由方程系数直接把根表示出来的公式。这个公式早在公元9世纪由中亚细亚的阿尔·花拉子模给出。

用求根公式法解一元二次方程的一般步骤为：

①把方程化成一般形式 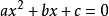 ，侍盯确定 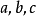 的值（注意符号）；

②求出判别式 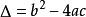 的值，判断根的情况；

③在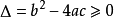  

（注：此处△读“德尔塔”）的前提下，把 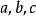 的值代入公式  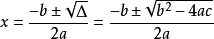进行计算，求出方程的根。

一元二次方程成立必须同时满足三个条件：

①是整式方程，即等号两边都是整式，桥核方程中如果有分母；且未知数在分母上，那么这个方程就是分式方程，不是一元二次方程，方程中如果有根号，且未知数在根号内，那么这个方程也不是一元二次方程（是无理方程）。

②只含有一个未知数；

③未知数项的最高次数是2。

扩展资料：

利用一元二次方程根的判别式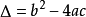（  ）可以判断方程的根的情况 。

一元二次方程 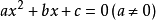 的根与老消和根的判别式 有如下关系：

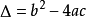
①当 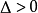 时，方程有两个不相等的实数根；

②当 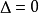 时，方程有两个相等的实数根；

③当 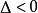 时，方程无实数根，但有2个共轭复根。

上述结论反过来也成立。

因式分解法即利用因式分解求出方程的解的方法 。

因式分解法解一元二次方程的一般步骤如下：

①移项，使方程的右边化为零；

②将方程的左边转化为两个一元一次方程的乘积；

③令每个因式分别为零；

④括号中  ，它们的解就都是原方程的解。

参考资料：百度百科---一元二次方程