怎么解一元三次方程
的有关信息介绍如下:一元三次方程的求根公式称为“卡尔丹诺公式”。 一元三次方程的一般形式迟御是 x3+sx2+tx+u=0 。
如作一个横坐标平移y=x+s/3,那么就可以把方程的二次项消去。所以只要考虑形如 x3=px+q
的三次方程。
例子:
假设方程的解x可以写成x=a-b的形式,这里a和b是待定的参数。
代入方程
a3-3a2b+3ab2-b3=p(a-b)+q
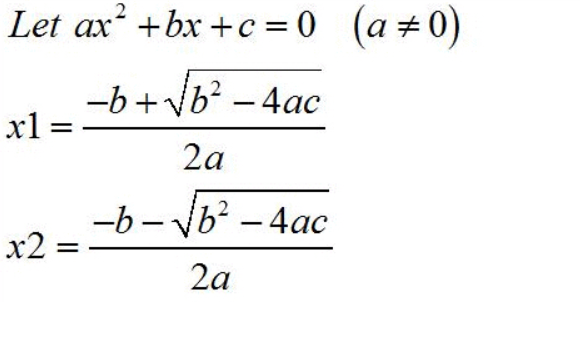
整理得到
a3-b3 =(a-b)(p+3ab)+q
由二次方程理论可知含兄,一定可以适当选取a和b,使得在x=a-b的同时, 3ab+p=0。这样上式就成为 a3-b3=q 两边各乘以27a3,就得到 27a6-27a3b3=27qa3 。
由p=-3ab可知 ,27a6 + p = 27qa3 这是一个关于a3的二次方程,所以可以解得a。
扩展资料
含有二次项但不含有一次项的一元三次方程,经过代换后可以消掉二次项,但是却会冒出一次项出来。
对于谈旦袭三次多项式,配立方,其结果除了完全立方项,后面既可以有常数项,也可以有一次项。一个自然的想法就是如何将一般的三次方程化为不带二次项的三次方程。
参考资料来源:百度百科-一元三次方程求根公式

