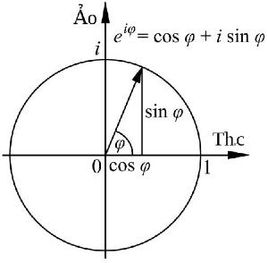
Simone欧拉常数为什么这么定义
的有关信息介绍如下：欧拉常数（Euler-Mascheroni constant)
欧拉-马歇罗尼常数(Euler-Mascheroni constant)是一个主要应用于数论的数学常数裂凳。它的定义是调和级数与自然对数的差值的极限。
由无穷级数理论可知蚂山，调和级数 是发散的。但可以证明，
存在极限。由不等式 可得
故 有下界。闷源中而
再一次根据不等式 ，取 ，即可得
所以 单调递减。由单调有界数列极限定理，可知 必有极限，即
存在。该极限被称作欧拉常数，现在通常将该常数记为γ。
向左转|向右转
