如何证明马鞍面是直纹面

如何证明马鞍面是直纹面

有一种构造马鞍面搏冲(双曲抛物面)的方法：取一个平面α与一对异面直线a, b都相交,则所有与α平行并与a, b都相交的直线的轨迹就是马鞍面。

取一个平面α与一对异面直线a,b都相交，则所有与α平行并与a,b都相交的直线的轨迹就是马鞍面。

这些直线就给出了马鞍面上的两族直母线中的一族。

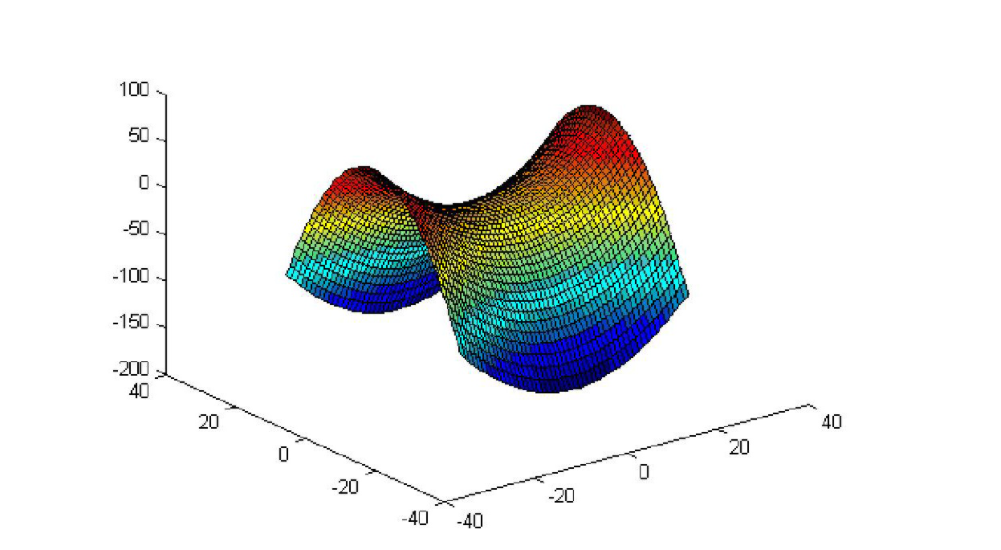
可以看到马鞍面上的一族直母线都与同一个平面平行，不同于锥面和单叶双曲面。

单彼此之间并不平行，不同于柱面。

直纹面简介：

直纹面可以描述为由移动的直线扫过的一组点。例如，通过保持线的一个点固定而沿着圆移动另一个点来形成锥体。如果通过其每个点都有两条不同的线，那么表面是双重的。双曲抛物面和一张双曲面是双重曲面。

被刻纹或再次刻纹的材料由投影图保留，因此是投影几何的概念。在代数几何尺度神世表面有时被认为是在场上的仿射或投影空间中的表面，但它们有时被认为是抽象代数曲面，而不嵌入仿射或投影空间，在这游银肢种情况下，“直线”被理解为意味着仿射线或投影线。