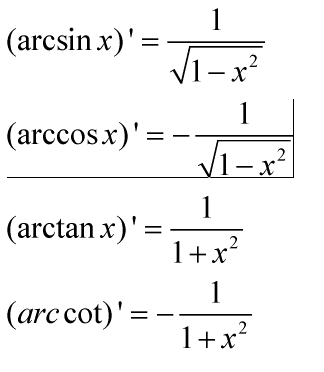
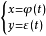二重积分求导

二重积分求导

将一元函数积分推广来看对于连续函数 f(x,y) 如何求二重积分. 每个二重积分都可以方便地用定积分的方法分步进行计算。

矩形区域上的二重积分

设 f(x,y) 在矩形区域 R: a<=x<=b, c<=y<=d 上有定义。 如果 R 被分别平行于 x 轴和 y 轴的直线网格所划分成许多小芹耐块面积 ∆ A="∆ x∆ y" 。

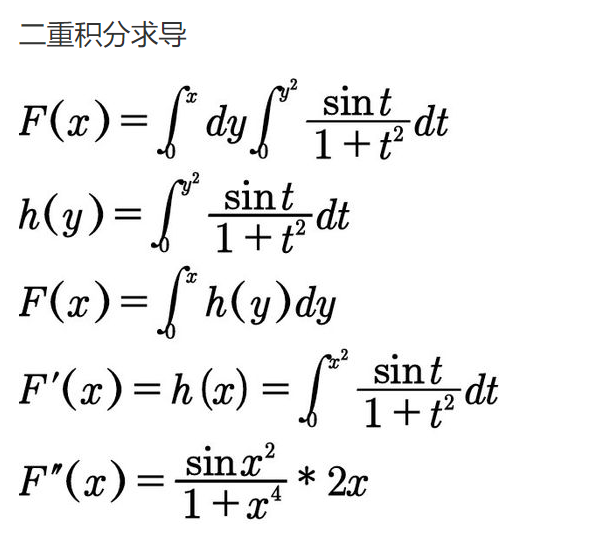
扩展资料

对直角坐标来说，主要考点有两个：

一是积分次序的选择，基本原则有两个：一是信咐看区域，选择的积分次序一定要便于定限，说得更具体一点，也就是要尽量避免分类讨论;

二是看函数，要尽量使第一步的积分简单，选择积分次序的最终目的肯定是希望是积分尽可能地好算一些，实践表明，大多数时候，只要让二重积分第一步的积分尽可能简单，那整个积分过程也会比较简洁；

所以在拿到一个二重积分之后，可以根据它的被积函数考虑一下第一步把哪个变量看成常数更有利于计算，从而确定积分次序。

二是定限，完成定限之后，二嫌坦春重积分就被化为了两次定积分，就可以直接计算了。