平行四边形的判定是什么？

平行四边形的判定是什么？

平行四边形的判定

1．一个四边形如果它的一组对边平行且相等那么它就是平行四边形。

2．一个四边形如果它的两组对边相等那么它就是平行四边形。

3．一个四边形如果它的两组对边平行那么它就是平行四边形。

4．一个四边形如果它的对角相等那么它就是平行四边形。

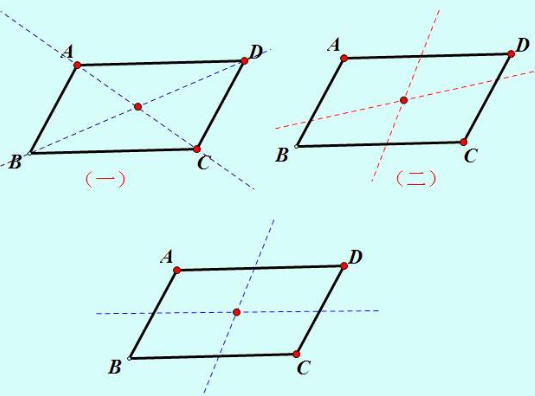
5．一个四边形如果它的对角线相互平分那么它就是平行四边形。

平行四边形的特点是对边相等，对边平行，对角相等，对角线相互平分，邻角互补。

平行四边形的对边是平行的（根据定义），因此永远不会相交槐粗。

平行四边形的面积是由其对角线之一创建的三角形的面积的两倍。

平行四边形的面积也等于两个相邻边的矢量交叉乘积的大小。

任何通过平行四边形中点的线将该区域平分。

任何非简并仿射变换都采用平行四边形的平行四边形。

平行四边形具有2阶（至180°）的旋转对称性（如果是正方形则为4阶）。如果它铅粗镇也具有两行反射对称性，那么凳誉它必须是菱形或长方形（非矩形矩形）。如果它有四行反射对称，它是一个正方形。