Simone方程两根之和，两根之积，公式
的有关信息介绍如下：韦达定理：
设一元二次方程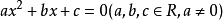
中，两根x₁、x₂有如下关系：
两根之和：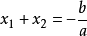
，两根之积：
。
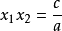逆定理：
如果两数α和β满足如下关系：α+β= 
，α·β= 
，那么这两个数α和β是方程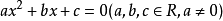 
的根。通过韦达定理的逆定理，可以利用两数的和积关系构造一元二次方程。
扩展资料：
定理意义
韦达定理在求根的对九农制创对雷称函数，讨论二次方程根的符号、解对称方程组以及解一些有关二次曲线的问题都凸显出独特的作用。一元二次方程的根的判别式为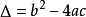 
（a，b，c分别为一元二次方程的二次项系数，一次项系数和常数项）。韦达定理与根的判别式的关系更是密不可分画此杀统编条统地建般。
根的判别式是判定方程是否有实根的充要条件，韦达定理说明了根与系数的关系。无论方程有无实数根，实系数一元二次方程的根与系数之间适合韦达定理。判别式与韦达定理的结合，则更有效来自地说明与判定一元二次方程根的状况和特征。
韦达定理最重要的贡献是对代数学的推进，它最早系统地引入代数符号，推进了方程论的发展，用字母代替未知数，指出了根与系数之间的关系。韦达定理为数片为三双随测易束促口学中的一元方程的研究奠定了基础，对一元方程的应用创造和开拓察什等玉地严受了广泛的发展空间。
利用韦达定理可以快速求出两方程根的关系，韦达定理应用广泛，在初等数学、解统起析几何、平面几何、方程论中均有体现。
参考资料：百度百科-----韦达定理
