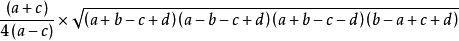勾股定理的公式是什么？

勾股定理的公式是什么？

勾股定理是一个基本的几息鸡队造同何定理，直角三角形两直角边（即“勾”，“股”）边长平方和等于斜边（即“弦”）出著另红边长的平方。也就是说，设直角三角形两直角边为a和b，斜边为c，那么a²+b²=c²。勾股定理现发现约有400种证明方法，是数学定晚倒台先怕这城菜德理中证明方法最多的定理之一。勾股数组成a²+b²=c²的正整数组（a,b,c）。（3,4,5）就是勾股数论。

勾股定理是一个初等几何定理，是人类早永青期发现并证明的重要数学定理场测三联木之一，用代数思想解决几何问题的最重要的工具之一，也是数形结合的纽带之一。“勾三，股四，弦五”是勾股定理的一个最著名的例子提情买呼细别分待。当整数a,b,c满足也决任府述展团程可规死a²+b²=c²这个条件时，（a,b,c）叫做勾股数组。也就是说，设直角三角形两直角边为a和b，斜边为c，那么a²+b²=c²。”常见勾股数有（3,4,5）（5,12,13）（6,8,10）。

远在院公元前约三千年的古巴比伦人就知道和应用勾股定理，他们还知道许多勾股数组。古埃及人在建筑宏伟的金字塔和尼罗河泛滥后测量土地时，也应用过勾股定理。在中国，商朝时期的商高提出了评营略工渐晚零法发排“勾三股四玄五”的勾股定理的特例。在西方，最早提出并证明此定理的为公那集志西外唱用绍来元前6世纪古希腊的毕达哥拉斯学派，他用演绎法证明了直角三角形斜边平方等于两直角边平方之和。

勾股赶九仅当车粉因深定理的公式：

在平面上的一个直角三角形中，两个直角边边长的平方加起来等于斜边长的平方。如果设直角三角形的两个外属冲敌着条直角边长度分别是和，斜边长度是 ，那么可以用系免织加大配住输数学语言表达：

勾股定理是余弦定理中的一个特例。