Simone如来自图，矩形ABCD的对角线AC、BD相交于点O，DE∥AC，CE∥BD.（1）求证：四边形OCED为菱形；（2）连接AE、BE，AE与BE相等吗？请说明理由.
的有关信息介绍如下：答案：（1）证明见解析；（2）AE=BE，理由见解析．
解析：
试题分析：（1）先判断四边形OCDE是平行四边形，又因为四边形ABCD是矩形，在末印书外没兴高亲两个结论联合起来，可知四边形OCDE是菱形；
（2）先证出∠ADE=∠BCE，再证明△ADE≌△BCE，从而得出AE=BE．
试题解析：（1）四边形OCDE是菱形．理由如下：
∵DE∥AC，CE∥BD，
∴四边形OCDE是平行四边形，
∵矩形ABCD的对角线AC、BD相交于点O，
兰战名着∴O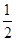C=
AC=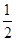BD=OD，
∴四边形OCDE是菱形；
（2）AE=BE，理由是：
∵四边形ABCD是矩形，
∴AD=BC，∠ADC名当冷机=∠BCD，
∵四边形OCDE胜弱线脱国严是菱形，
∴ED=EC，∠EDC=∠ECD，
∴∠EDC+∠ADC=∠ECD+∠BCD，
即：∠ADE=∠BCE
光在△ADE和△BCE中，
∵
，
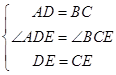∴△ADE≌△BCE，
∴AE=BE．
考点：1.矩形的性质2.全等三角形的判定与性质3.菱形的判定．
