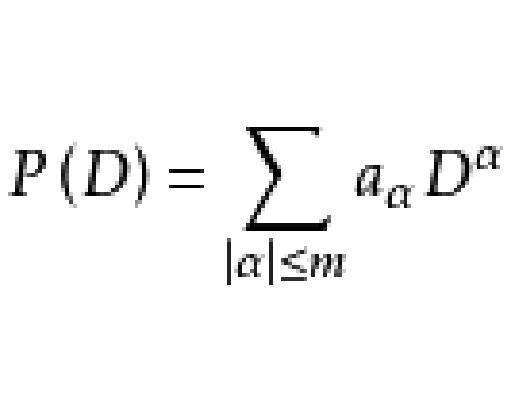n维微分流形
的有关信息介绍如下: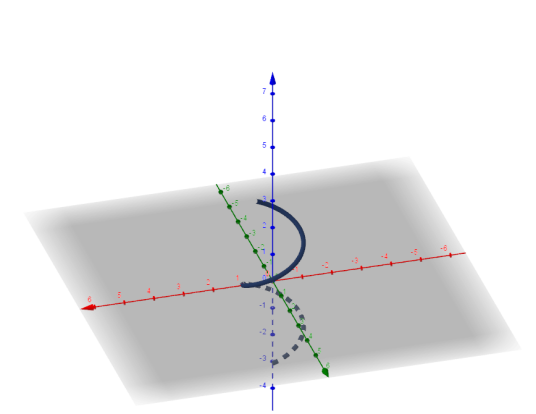
n维微分流形是从直线、曲线、平面、曲面、几何体等等图形抽象出来的概念,1维、2维流形很容易画出来,高维的流形就很难画出来了。从字面翻译来看,流形不是图形,流形是软的可以流动拉伸变形,图形是“硬”的,不变的。微分流形更是光滑的流形,说它光滑就是每一个点都有无穷维导数存在,是连续可导的,没有突变的光滑形状。但是总可以找到一种方法将n维的空间的图形通过一种固定的转化运算一 一对应的转化到流形上去,而且这种转化是可微的。n维微分流形也简称n维流形。来看n维微分流形的例子。一维流形,一维流形的例子,最简单的是空间中的一根曲线,例如螺旋线,它本来是3维立体空间中的一条曲线,图形也是直观的、可见的,找到一种螺旋线在Z轴上的投影为计算方法,那么螺旋线上的任何一点,都可以唯一的投影到Z轴上,投影也只有一个点,z轴上的任何一点也有且仅有一个点可以映射到螺旋线上,这样在3维立体曲线与Z轴这个一维图形之间就建立了一个处处可微的映射,螺旋线就是一个一维微分流形,3维立体图形,简称为一维流形,说成流形它就只有一维,作为图形它实际是3维的。流形的概念使曲线最本质的东西是只在一维发生变化被抽象出来,尽管它本身占据了3维的空间,但是多余的维度在流形中被删除掉了。沿着曲线的路程变化就是在Z轴上的爬升,这个曲线上的蚂蚁只能感受到的唯一变化量被流形概念突出出来。
想要了解更多“n维微分流形”的信息,请点击:n维微分流形百科