张角定理的证明

张角定理的证明

证法1：

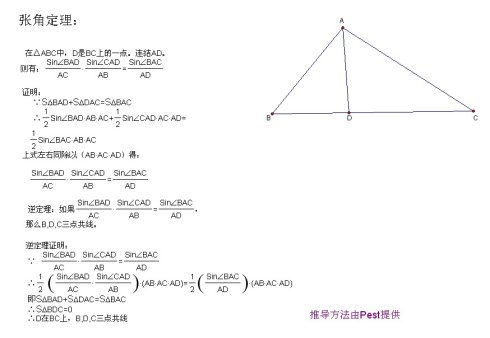
设∠1=∠BAD，∠2=∠CAD

由分角定理，

S△ABD/S△ABC=BD/BC=(AD/AC)*(sin∠1/sin∠BAC)

→ (BD/BC)*(sin∠BAC/AD)=sin∠1/AC (1.1)

S△ACD/S△ABC=CD/BC=(AD/AB)*(sin∠2/sin∠BAC)

→ (CD/BC)*(sin∠BAC/AD)=sin∠2/AB (1.2)

(1.1)式+(1.2)式即得 sin∠1/AC+sin∠2/AB=sin∠BAC/AD。

证法尘消2：

由正弦定理，

AD/sinB=BD/sin∠1，　(2.1)

AD/sinC=CD/sin∠2，　(2.2)

AB/sinC=BC/sin(∠1+∠2)，　(2.3)

AC/sinB=BC/sin(∠1+∠2)；　(2.4)

那么由(2.1)，(2.2)，BD=ADsin∠1/sinB，CD=ADsin∠2/sinC，从带启而

BC=BD+CD=AD(sin∠1/sinB+sin∠2/sinC)　(2.5)

由(2.3)，(2.4)，知sin∠1/AC=sin∠1sin(∠1+∠2) / BCsinB，sin∠2/AB=sin∠2sin(∠1+∠2) / BCsinC。

将以上两式相加，并将(2.5)代入即可。

证法3：

由面积蠢兄如和得：

0.5sin∠BAD*BA*AD+0.5sin∠DAC*DA*AC=0.5sin∠BAC*BA*AC