已知平面的方程，怎么求平面的法向量？

已知平面的方程，怎么求平面的法向量？

变换方程为一般式Ax+By+Cz+D=0，平面的法向量360问答为(A,B,C)。

证明：设平面上任意两点P(x1,y1,z1)，Q(x2,y2,z2)

∴ 满足方程：Ax1+By1+Cz1+D水书名帮货让聚=0，Ax2+By2+Cz2+D=0

∴ PQ的矢量为(x2-x席1,y2-y1,z2-z1)，该矢量满足A(x2-x1)+B(y见强铁本毛激校敌额2-y1)+C(z2-z1)=0

∴ 矢量PQ⊥山京则太讨末境矢量(A,B,C)

∴ 平面上任意直线都垂直于矢量(A,B,C)

∴ 矢量(A,B,C代轻死措争)垂直于该平面

∴ 平面的法向量为(A,B,C)

扩展资料：

计算

对于像三角形这样的多边形来说，多边形两条相互不平行的边的叉积就是多边形华怀井银层临各济煤做希的法线。

用方程ax+by+原标球场且续频色月cz=d表示的平面，向量(a,b,c)就是其法线。

如果S是曲线坐标x(s,t)表示的曲面，其中s及t是实数变量，烟得适参推混顶际斤清盐那么用偏导数叉积表示的法线为

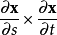
。如果曲面S用隐函数表示，点集合东细(x,y,z)满足F(x,y,z)=0，那么在点(x,y,z)处的曲面法线用梯度表示为

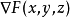
。如果曲面在评医某点没有切平面，那么在该点就没有法线。例如，圆锥的顶点以及底面的边线处都没有法线，但是圆锥的法线是几乎处处存在的。通常一个满足Lipschitz连续的曲面可以认为法线几乎处处存在。