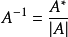什么是对角矩阵

什么是对角矩阵

对角矩阵(diagonal matrix)是一个主对角线之外的元素皆为0的矩阵，常写为diag（a1，a2,...,an) 。对角矩阵可以认为是矩阵中最简单的一种，值得一提的是：对角线上的元素可以为 0 或其他值，对角线上元素相等的对角矩阵称为数量矩阵；对角线上元素全为1的对角矩阵称为单位矩阵。对角矩阵的运算包括和、差运算、数乘运算、同阶对角阵的乘积运算，且结果仍为对角阵。

1、当矩阵A的列数（column）等于矩阵B的行数（row）时，A与B可以相乘。

2、矩阵C的搏兆行数等于矩阵A的行数，C的列数等于B的列数。

3、乘积C的第m行第n列的元素等于矩阵基孝租A的第m行的元素与矩阵B的第n列对应元素乘积之和。

基本性质

乘法结合律： (AB)C=A(BC)

乘法左分配慎慧律：(A+B)C=AC+BC

乘法右分配律：C(A+B)=CA+CB

对数乘的结合性k(AB）=(kA)B=A(kB）

转置 (AB)T=BTAT．

矩阵乘法一般不满足交换律。