余切函数的余切函数的图像

余切函数的余切函数的图像

余拆皮切函数的图像如下所示：

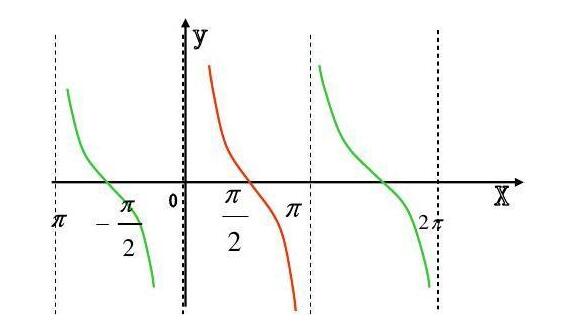
任意角终边上除顶点外的任一点的横坐标除以该点的非零纵坐标,角的顶点与平面直角坐标系的原点重合,而该角的始边宽裂则与正x轴重合。简单点理解:直角三角形任意一锐角的邻边和对边的比,叫做该锐角的余切。

余切表示用“cot+角度”，如：30°的余切表示为cot 30°；角A的余切表示为cot A。旧时用ctg A来表示余切，和cot A是一样的。假设∠A的对边为a、邻边为b，那么cot A= b/a（即邻边比对边）。

扩展资料：

余切的发展历史：

叙利亚天文学家、数学家阿尔巴坦尼(850-929)于920年左右，制成了自旅巧差0到90度相隔1度的余切表。

14世纪中叶，成吉思汗的后裔，中亚细亚的阿鲁伯(1393--1449)组织了大规模的天文观测和数学用表的计算，他的正弦表精确到小数9位，他还制作了30到45度之间相隔为1"，45到90度的相隔为5"7'的正切表。

英国数学家、坎特伯雷大主教布拉瓦丁(1290-1349)首先把正切、余切引入他的三角计算之中。