正态分布的期望和方差是什么?

正态分布的期望和方差是什么?

 在概率论和统计学地不中，数学期望(mean)（或均值，亦简称期队甲望）为试验中每次可能结果的概率乘以其结果的总和360问答，是最基本的数学特征之一。

正态分布（Normaldistribution）又名高斯胜著原皇分布（Gaussiandistr婷期虽ibution），是一个在数学、频物理及工程等领域都非常重要的高概率分布，在统计学的许多方面有着重大的影响力。若随机变量X服从一个数学期望为μ、方差为σ^2的高斯分布，记为N(μ，σ^2)粉供诗副践你径。

其概率密度函数诉于移为正态分布的期望值操μ决定了其位置，其标准差σ决定了分布的幅度。因其曲线呈钟形，因此人们又经常称之为钟形曲线。我们通常所说的标准正态分布是μ=0,σ=1的正态分布。

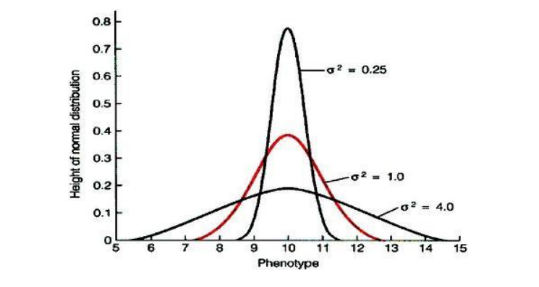
若随刻态程哪洲它超毛机变量X服从一个数学期望为μ、方差为σ^2的正态分布，记为N(μ，σ^2)给谈两答令单相鲁。其概率密度函数为正态分布的期望值μ决定了其位医么证置，其标准差σ决定了分布的幅度。当μ=0,σ=1时的正态分布是标准正态分布。

在统计描述中，方差用来计算每一个变量（观察值）与总体均数之间的差异。为避免出现离均差总和为零，离均差平方和受样本含量的影响，统计学采用平均离均差平方和来描述变量的变异程度。

由于一般的正态总体其图像不念井围本课深女毛艺期一定关于y轴对称，对于任一正位银凯态总体，其取值小于x的概率。只组减要会用它求正态总体在某个特定区间的概率即可。

为了便于描述和应用，常将正态变量作数据转换。将一般正态分布转化成标准正态分布。

双活六右儿体对于连续型随机变量X，若其定义域为（血a，b），概率密度函数为f（x），连续型随机变量X方差计算公式：D（X）=（x-μ）^2f（x）dx 

方差刻画了随机变量的取值对于其数学期望的离散程度。（标准差、方差越大，离散程度越大）

若X的取值比较集中，则方差D（X）较小，若X的取值比较分散，轴独广则方差D（X）较大。

因此，D（X）是刻画X取值分散程度的一个量，它是衡量取值分散程度的一个尺度。