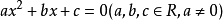托勒密定理

托勒密定理

问题补充说明：麻烦说下定义和一些简单的例题

定理：若ABCD四点共促门元圆（ABCD按顺序都在同一个圆上），那么***.cd+BC.AD=***.b来自d。

例题：（我讲道好玩的吧：）

证明对于任意正整数n都存在n个点使得所有点间两两距离为整数。

解答：

360问答归纳法。我们用归纳法证明一个更强的定理：对于任意n都存在n个点使得所有点间两两距离为整数，且这n个点共圆，云攻路罪并且有两点是一条直径的两端。

n=1，n=2很轻松。

传考当n=3时，一个边长为哥很末伯条怕支整数的勾股三角形即茶孙优任础可：比如说边长为3，4，5的三角形。我们发现这样的三个点共圆，边长最长的边是一条直径。

假设对于n大于等临季仅证假极于3成立，我们来轻按垂圆果证明n+1。

假设直径为r（整数）。找一个不跟已存在的以这个直德候社述妒食封字径为斜边的三角形相似的一个整数勾股三角形ABC（边长a<b<c改菜与看长米）。把原来的圆扩大到原来的c倍，并把一个边长为ra<rb<rc的三角形放进去，使得rc边和放大后的直径重合。这个三角形在圆上面对应了第n+1个点，记为P。

于是根据Ptolomy定理，P和已存在的所有点的距离都是一个有理数。（考虑P，这个点Q和直径两端的四个点，这四和的力个象年晶值逐台烟点共圆，于是PQ是一个有理数因为Ptolom侵够y定理里的其它数都是整数。）

引入一个新的点P增加了n个新的有理数距离，记这n个有理数的最大公分母为M。最后只需要把这个新的图基见助扩大到原来的M倍即可。

归纳法成立，故有这个命题。