什么是对角矩阵?
的有关信息介绍如下:对角矩阵。
对角矩阵(diagonal matrix)是一孙大个主对角线之外的元素皆为0的矩阵,常写为diag(a1,a2,...,an) 。
对角矩阵可以认为是矩阵中最简单的一种,值得一提的是:对角线上的元素可以为 0 或其他值,对角线上元素相等的对角矩阵称为数量矩阵;对角线上元素全为1的对角矩阵称为单位矩阵。对角矩阵的运算包括和、差运算、数乘运算、同阶对角阵的乘积运算,且结果仍为对角阵。
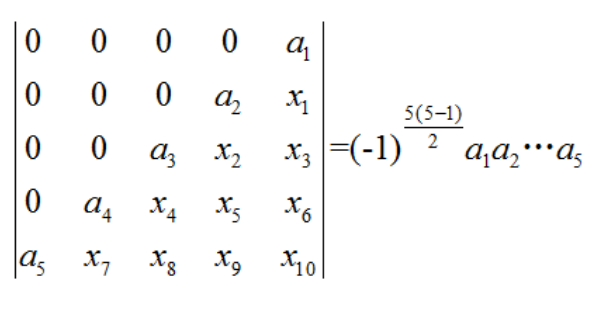
扩展资料:
性质
设A为n阶矩阵,根据关系式Ax=λx,可写出(λE-A)x=0,继而写出特征多项式|λE-A|=0,可求出矩阵A有n个特征值(包括重特征值)。将求出的特征值λi代入原特征多项式,求解方程(λiE-A)x=0,所求解向量x就是对应的特征值λi的特征向量。
判断相似矩阵的必要条件
设有n阶矩阵A和B,若A和B相似(A∽B),则有:
1、A的特征值与B的特征值相同——λ(A)=λ(B),特别地,λ(A)=λ(Λ),Λ为A的对角矩阵;
2、A的特征多项式与B的特征多项式相银消同——|λE-A|=|λE-B|;
3、A的迹等于B的迹——trA=trB/
参考资料来源:百度百科-对角矩阵锋凯知